Знаменатель дробей дожен быть ≠ 0, поэтому
x≠1, x≠2 и x ≠0
приводим к одному знаменателю x²(x-1)²(x-2)²

x²(x-2)²+x²(x-1)²- 2(x-1)²(x-2)²=0
(x²-2x)²+(x²-x)²- 2((x-1)(x-2))²=0
x⁴-4x³+4x²+x⁴-2x³+x²-2(x²-2x-x+2)²=0
2x⁴-6x³+5x²-2(x²-3x+2)²=0
2x⁴-6x³+5x²-2(x⁴-3x³+2x²-3x³+9x²-6x+2x²-6x+4)=0
2x⁴-6x³+5x²-2(x⁴-6x³+13x²-12x+4)=0
2x⁴-6x³+5x²-2x⁴+12x³-26x²+24x-8=0
6x³-21x²+24x-8=0
теперь найдем максимумы и минимумы функции
y(x)=6x³-21x²+24x-8
y'(x)=18x-42x+24
18x-42x+24=0
9x-21x+12=0
D=21²-4*9*12=9
√D=3
x₁=(21-3)/18=1
x₂=(21+3)/18=4/3
y(x₁)=y(1)=6-21+24-8=1 максимум
y(x₂)=y(4/3)=6(3/4)³-21(4/3)²+24(4/3)-8=0,89 минимум
y(-∞)=-∞
y(∞)=∞
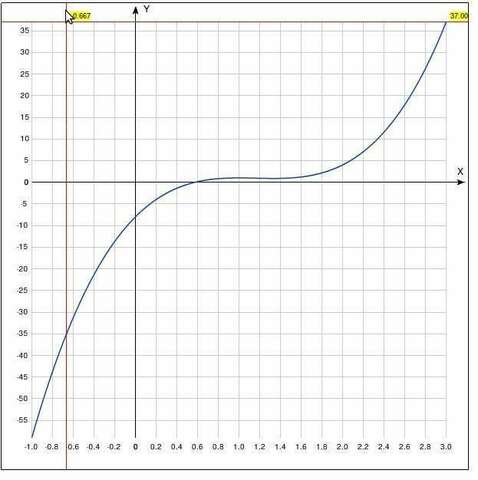
получаем график как на рисунке.
видно, что график пересекает y(x) ось у=0 в одной точке, поэтому решение одно