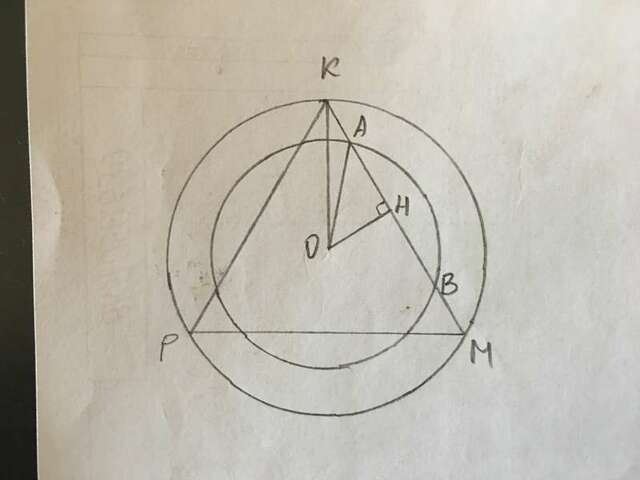
ΔKMP - правильный, КМ=10√3, АВ=КМ.
Радиус большей окружности: ОК=R=КМ/√3=10√3/√3=10.
ОН - радиус вписанной окружности в тр-ник КМP. r=R/2=5.
В равнобедренном тр-ке АОВ ОН⊥АВ, значит ОН - медиана. АН=НВ=АВ/2=5.
В прямоугольном тр-ке АОН АО=АН, значит он равнобедренный, значит ∠АОН=45°, следовательно ∠АОВ=90° (треугольники АОН и ВОН равны по трём сторонам).
АО=АН√2=5√2.
Формула площади сегмента окружности: S=((π·α°/180°)-sinα)·R²/2.
Площадь заштрихованного сегмента, ограниченного хордой AB, окружности с радиусом АО:
S=((π·90/180)-sin90)·(5√2)²/2=((π/2)-1)·50/2=25(π-2)/2.
Так как окружности с радиусами ОК и ОА концентрические и треугольник КМP правильный, то заштрихованные сегменты равны.
Площадь всех заштрихованных сегментов (площадь искомой фигуры):
Sф=3S=75·(π-2)/2 (ед²)- это ответ.