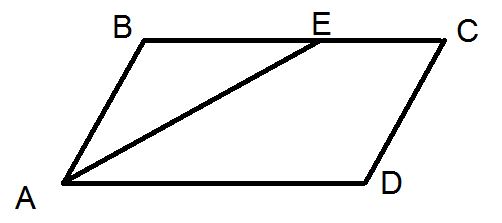
Угол BAE равен EAD (AE - биссектриса BAD)
BD параллельна AD (прямоугольник является параллелограммом по условию)
угол BEA равен EAD (смежные углы при пересечении параллельных прямых общей секущей прямой AE)
Следовательно углы BAE и BEA равны и треугольник BAE - равнобедренный, т.е.
|AB| = |EB|
Периметр параллелограмма равен
P = |AB| + |BC| + |CD| + |DA| = 2 * (|AB| + |BC|) =
= 2 * (|BE| + |BC|) = 2 * (|BE| + |BE| + |EC|) =
= 4 * |BE| + 2 * |EC|
По условию, биссектриса делит сторону на отрезки 12 и 7 см.
Если |BE| = 7 см, то периметр P = 4*7 + 2*12 = 52
Если |BE| = 12 см, то периметр P = 4*12 + 2*4 = 56