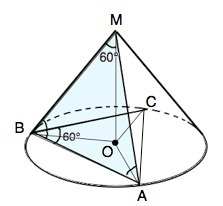
Обозначим вершину конуса М.
Соединив точки А и С, получим равнобедренный ∆ АВС с углом при В=60°, ⇒ ∆ АВС - равносторонний, для которого окружность, ограничивающая основание конуса - описанная.
По условию сечение АМВ - равносторонний треугольник, и стороны АВС равны его сторонам, т.к. АВ - общая их сторона.
S∆ АМВ=9√3
S ∆AMB=(a²√3):4 формула площади правильного треугольника. ⇒
(a²√3):4=9√3 ⇒ a²=4•9; a=√36=6
Формула радиуса описнной окружности R=a:√3
R=ВО=6:√3
Из ∆ ВОМ высота МО=√(BM*-BO*)=√(36-12)=2√6
Формула объема конуса V=S•h:3
S=πR²=π•36:3=12π
V=(12π•2√6):3=8π√6см³