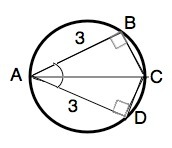
Окружность проведена через А, следовательно, А лежит на окружности.
АВ и АD - равные стороны вписанного угла ВАD, поэтому его биссектриса АС проходит через центр окружности и является её диаметром .
∠АВС=∠АDC=90°- опираются на диаметр.
Треугольники АВС и АBD равны по катету и гипотенузе, поэтому площадь каждого равна половине площади четырехугольника АВСD - равна 1,5√3
Площадь прямоугольного треугольника равна половине произведения его катетов.
S ∆ АВС=АВ•BC:2
BC=2S:AB=3√3):3=√3
ВС:АВ=tg∠ВАС
tg∠BAC=√3):3=1:√3. Это тангенс угла 30°.
Тогда, так как ∠ВАС=∠DAC, угол ВАD=60°
* * *
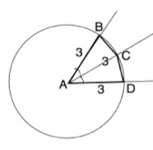
Если А - центр окружности, результат будет тот же, но решение немного другим Тогда АВ=АС=AD=R
AB+AD=6 AB=AD=AC=6:2=3⇒ R=3
АС - биссектриса. ∠ВАС=∠DAC⇒∆ ABC=∆ ADC по 1 признаку равенства треугольников.
S∆ ВАС=S∆DAC= S ABCD:2
sin BAC=2•SBAC:AB²⇒
sin BAC=3√3):9=√3:3=1/√3 - это синус 30°
Тогда, т.к. АС биссектриса, угол ВАD=60° Это ответ.
----------