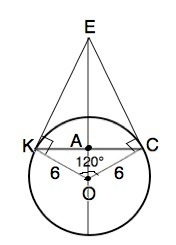
Сумма углов четырехугольника =360°
В четырехугольнике ОКЕС углы ЕКО=ЕСО=90° ( свойство радиуса, проведенного в точку касания)
Угол КЕС=360°-2•90°-120°=60°
По свойству отрезков касательных из одной точки КЕ=СЕ.
∆ КЕС - равнобедренный, его углы при КС равны (180°-60°):2=60° -
∆ КЕС равносторонний.
∆ КОС - равнобедренный ( стороны - радиусы).
Углы при КС=90°- 60°=30°
КЕ=СЕ, КО=СО, ЕО - общая. ∆ ЕКО=∆ ЕСО.
ЕО - биссектриса угла КЕС.
Угол ОЕС =30°
∆ ОЕС - прямоугольный.
Радиус ОС ( катет) противолежит углу 30°. ⇒
ОЕ=2•OC=12 см (свойство угла 30°).
КА=СА, ЕА медиана и высота ∆ КЕС,⇒ ЕО ⊥ АС.
В прямоугольном Δ АОС угол ОСА=30°⇒
ОА=ОС•sin30°=6•0,5=3 см