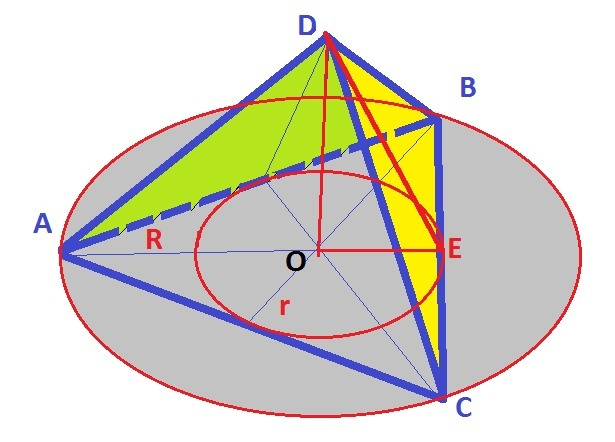
Делаем рисунок.
ДАНО
АО - R = √3 - радиус описанной окружности.
DE = 2√7 - апофема.
НАЙТИ
V = ? - объем пирамиды.
РЕШЕНИЕ
Площадь основания в равностороннем треугольнике.
S= √3/4*a²
Радиус описанной окружности по формуле
R = a/√3 = √3
Находим длину ребра в основании.
a = √3*√3 = 3.
Площадь основания в равностороннем треугольнике.
S= √3/4*a² = 9√3/4
Радиус описанной окружности
r = ОЕ = R/2 = √3/2
Находим высоту пирамиды из треугольника DOE.
DO² = (2√7)² - (√3/2)² = 14 - 3/4 = 13 1/4
h = √13.25 ≈ 3.64
V = 1/3* S * h = 1/3* 9/4*√3*√13.25 ≈ 0.75*1.73*3.64 ≈ 4.728 - ОТВЕТ