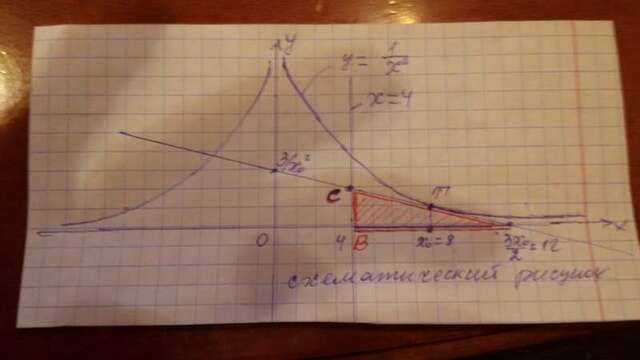
Касательная к графику функции y=1/x² такова, что абсцисса c точки касания лежит на отрезке от 5 до 9. При каком значении c площадь треугольника, ограниченного этой касательной, осью OX и прямой x= 4 , будет наибольшей ? Чему равна эта наибольшая площадь?
-----------
f(x) = 1/x²
касательная к графику функции y=f(x) в точке ( x₀, f '(x₀)), где 5 < x</span>₀ < 9 ;
y = 0 (уравнения оси абсцисс_ OX)
x= 4.
-----------
Схематическая картина изображена в прикрепленном файле
------------------
Уравнение касательной к графику функции y = f(x) в точке ( x₀, f '(x₀)) имеет вид y = f '(x₀) (x - x₀) + f (x₀).
f (x₀) = 1/x₀² ; f '(x) =( 1/x² )' =( x⁻² )' = -2*(x⁻²⁻¹ ) = -2*(x⁻³) = -2/ x³ ; f '(x₀) =-2/x₀³.
y =-(2/x₀³)* (x - x₀) + 1/x₀² ⇔ y = - (2/x₀³)* x + 3/x₀² ;
Точка пересечения касательной с осью абсцисс (обозначаем через А) :
у = 0 ⇒ x =3x₀ /2
* * * А(3x₀ /2: 0) * * *
Точка пересечения касательной с прямой x = 4 (обозначаем через C) :
y(C) = - (2/x₀³)* 4 + 3/x₀² = -8/x₀³+3/x₀² =(3x₀ -8) / x₀³
* * * C( 4; (3x₀ -8) / x₀³ ) ; B(4 ;0) * * *
S(x₀)=S(∆ABC)=(1/2)* AB*BC=(1/2)*(3x₀ /2-4)*(3x₀-8)/x₀³ =(1/4)*(3x₀ -8)² /x₀³
S(x₀) = (1/4)*(3x₀ -8)² /x₀³ .
Обозначаем F(x₀) =(3x₀ -8)² /x₀³ и определяем x₀ при которой функция F(x₀) принимает свое максимальное значение .
F' (x₀) = ( (3x₀ -8)² /x₀³ ) ' =( 2(3x₀ -8)*3*x₀³ - (3x₀ -8)²*3x₀² ) / x₀⁶ =
3x₀²(3x₀ -8)*(2x₀ - 3x₀ +8) ) / x₀⁶ =3(3x₀ -8)*(8 -x₀) / x₀⁴
F' (x₀) - + -
--------------------- 8/3 ------------------- 8 -------------------- * * * 8 ∈ (4;9 ) * * *
F(x₀) ↑
↑ max ↑
max (S(x₀))= S(8)= (1/4)*(3*8 -8)² /8³ = .(1/4)*8² (3 -1)² /8³ =(1/4)*4 /8 =1/8.
ответ : 1/8 ед. площ. ( проверить арифметику )
===================
Удачи !