Плоскости α и β параллельны. Через точки А и В плоскости α проведены параллельные прямые,...

Question

Плоскости α и β параллельны. Через точки А и В плоскости α проведены параллельные прямые, пересекающие плоскость β в точках А1 и В1 соответственно. А1А: АВ = 1: 3, АВ = 9 см. Найдите периметр А1АВВ1.

Answer 1

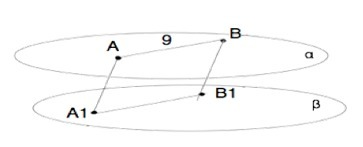
Через две параллельные прямые можно провести плоскость, и притом только одну. (теорема).

Точки А, А1, В и В1 лежат в плоскости АВВ1А1.  Эта плоскость пересекает параллельные плоскости α и β. 

Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны. 

Следовательно, АВ|║А1В1, и четырёхугольник АВВ1А1, противоположные стороны которого параллельны - параллелограмм. 

В параллелограмме противоположные стороны равны. 

А1А:АВ=1:3.⇒ АА1=АВ:3=9:3=3

Р (АВВ1А1=2(А1А+АВ)=2•(3+9)=24 см

---