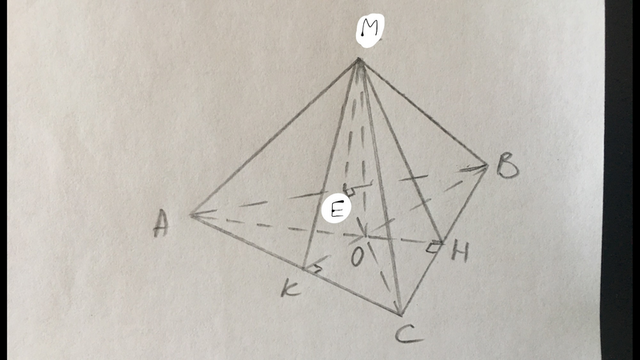
МАВС - пирамида. АВ=ВС=10, АС=12, l=5, l - апофема.
Так как точка М равноудалена от сторон основания пирамиды, то основание высоты МО точка О лежит в центре вписанной в основание окружности.
ВК - высота и медиана треугольника АВС. АК=КС=АС/2=12/2=6.
В тр-ке АВК ВК=√(АВ²-АК²)=√(10²-6²)=8.
Площадь треугольника АВС: S=АС·ВК/2=12·8/2=48.
ОК - радиус вписанной окружности. r=S/p, где р - полупериметр.
p=АВ+АК=10+6=16.
ОК=r=48/16=3.
В прямоугольном тр-ке МКО МО=√(МК²-ОК²)=√(5²-3²)=4 - это ответ.