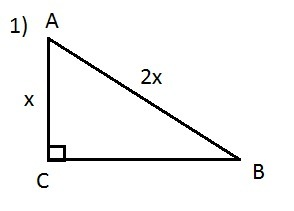
1) Пусть ΔАВС - прямоугольный, ∠С=90°, катет АС=х, гипотенуза АВ=2х. (см. рисунок 1)
cos∠A=AC/AB=x/(2x)=1/2, ∠A=60°.
∠B=90°-60°=30°.
Ответ: 60°, 30°.
2) Пусть х - коэффициент пропорциональности, тогда ∠1=х, ∠2=2х, ∠3=3х. Сумма углов треугольника равна 180°. Составляем уравнение:
х+2х+3х=180°;
6х=180°;
х=180°:6;
х=30°
∠1=30°, ∠2=2*30°=60°, ∠3=3*30°=90°.
Данный треугольник - прямоугольный.
Ответ: 30°, 60°,90°; прямоугольный.
3) Пусть х - меньший угол прямоугольного треугольника, тогда (х+10°) - больший. Сумма двух острых углов прямоугольного треугольника равна 90°. Составляем уравнение:
х+х+10°=90;
2х=90°-10°;
2х=80°;
х=40°.
Меньший угол равен 40°, больший угол 40°+10°=50°.
Ответ: 40°, 50°.