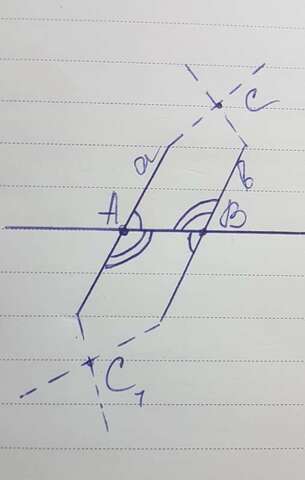
Теорема: если внутренние накрест лежащие углы равны или сумма внутренних односторонних углов равна 180°, То прямые параллельны.
доказательство: даны две прямые а и b образуют с секущей АВ разные внутренние накрест лежащие углы. Допустим, пусть прямые a и b не параллельны, и пересекаются в некоторой точке С. секущая AB разбивает плоскость на две полуплоскости. В одной из них лежит точка C. Построим треугольник АBС1, равный треугольнику ABC, с вершиной C1 в другой полуплоскости. По условию внутренние накрест лежащие углы при прямых а b и секущей AB равны. и соответствующие углы треугольников ABC и ВАС1 совершенной А и В равны, то они совпадают с внутренними накрест лежащими углами. значит прямая АС1 совпадает с прямой а, а прямая BC1 совпадает с прямой b. получается, что через точки C и C1 проходят две различные Прямые a и b. А это невозможно, значит, Прямые a и b параллельны. если у прямых a и b и секущей AB сумма внутренних односторонних углов равна 180°, То, внутренние накрест лежащие углы равны.