ДАНО
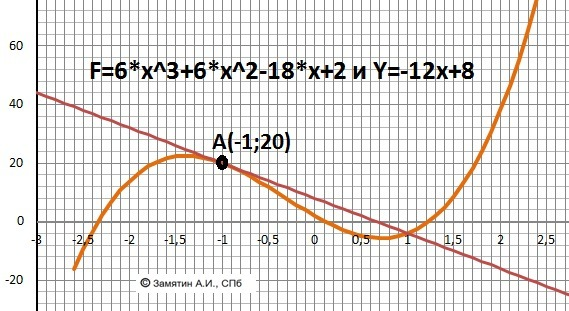
Y = 6*x³ + 6*x² - 18*x + 2 - функция
Хо = - 1 - точка касания.
НАЙТИ
Уравнение касательной.
РЕШЕНИЕ
Уравнение - по формуле
Y = Y(Xo) + Y'(Xo)*(X - Xo)
1) Y(Xo) = Y(-1) = -6 + 6 + 18 + 2 = 20.
Производная функции - расчет
2) Y'(x) = 6*3*x² + 6*2*x - 18 = 18*x² + 12x - 18
Значение производной в точке Хо.
3) Y'(-1) = 18 - 12 - 18 = - 12
Записываем уравнение касательной
4) Y = 20 - 12*(x - (-1)) = -12*x + 8 - ОТВЕТ
Дополнительно - в подарок - графики и функции и касательной.
Красиво и правильно.