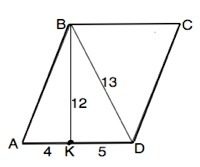
Отношение сторон треугольника 5:12:13 - из множества Пифагоровых троек для прямоугольных треугольников, (т.е. сочетание трех целых чисел, для которых верно равенство a²+b²=c²). Для доказательства проверим по т.Пифагора:
12²+5²=13²– верное равенство. Треугольник ВКD - прямоугольный. Тогда ВК ⊥ АD и является высотой параллелограмма.
Одна из формул площади параллелограмма S=a•h, где а - сторона параллелограмма, h - высота, проведенная к ней.
S=BK•AD=12•(4+5)=108 см²