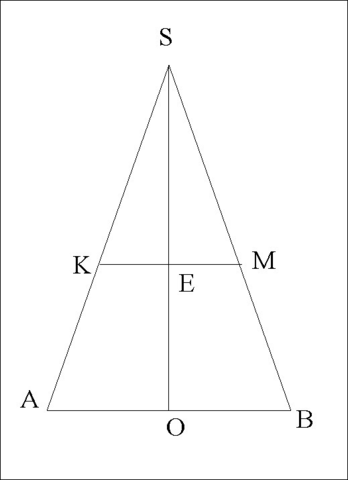
1.На чертеже осевое сечение пирамиды.
H = SO = 36
S = 400 см²
s =100 см²
EO-?
Решение
Так как сечение параллельно основанию, то треугольники в осевом сечении подобны между собой.
Площади подобных фигур относятся как квадраты их соответствующих линейных размеров.
Имеем соотношение: S : s = H² : h² , т.е.
S : s = (SO)² : (SE)²
(SE)² = s · (SO)² : S
(SE)² = 100 · 36² : 400 = 324
SE = √324 = 18см
OE = SO - SE = 36 - 18 = 18 см
Ответ: 18 см
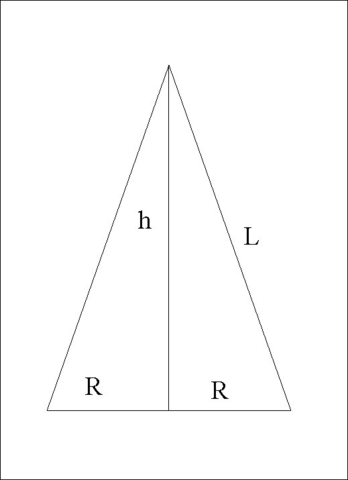
2. Дано:
R = 5cм;
h= 12 см
L-?
S-?
1) По теореме Пифагора L² = R² + h²
L² = 5² + 12² = 25 + 144 = 169
L = √169 = 13 см - длина образующей.
2) Осевое сечение - это треугольник, у которого боковые стороны равны образующим, а основание равно диаметру 2R.
Площадь треугольника равна половине произведения основания 2R на высоту h.
S = (2R·h)/2 = Rh
S = 5 · 12 = 60 см²
Ответ: L = 13 см; S = 60 см²