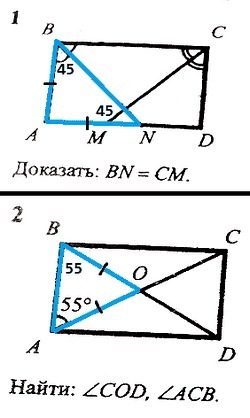
1) У прямоугольника все углы прямые. Биссектриса делит прямой угол на два угла по 45. Треугольник ABN - прямоугольный с углом 45, следовательно равнобедренный (другой острый угол равен 90-45=45, углы при основании равны), AB=AN. Аналогично СD=MD. Противоположные стороны прямоугольника равны: AB=CD. Прямоугольные треугольники ABN и MCD равны по двум катетам (AB=AN=СD=MD). Следовательно, их гипотенузы равны, BN=CM.
2) У прямоугольника все углы прямые, ∠ABC=90. ∠ACB=90-∠BAC=90-55=35 (сумма острых углов прямоугольного треугольника равна 90). Диагонали прямоугольника равны и точкой пересечения делятся пополам, AO=BO. Треугольник ABO - равнобедренный, ∠ABO=∠OAB=55. ∠BOA=180-∠ABO-∠OAB= 180-55*2=70. ∠COD=∠BOA=70 (вертикальные углы).