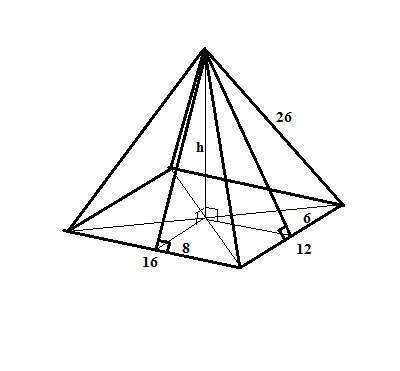
Боковые ребра пирамиды равны, значит вершина пирамиды проецируется в центр основания (пересечение диагоналей прямоугольника).
Грани пирамиды - по два равнобедренных треугольника с основаниями 16 см и 12 см и высотами √(26²-8²)=6√17см и √(26²-6²)=8√10 соответственно.
Значит Sбок=2*(S1+S2), где S1=(1/2)*16*6√17=48√17см и
S2=(1/2)*12*8√10см. То есть Sбок=96(√17+√10)см².
Высота пирамиды равна по Пифагору:
h=√(36*17-36)=√(36*(17-1))=2*3*4=24см или
h=√(64*10-64)=√(64*(10-1))=8*3=24см.
Объем пирамиды равен
V=(1/3)So*h = (1/3)*12*16*24=1536см³.
Ответ: Sбок=96(√17+√10)см², V=1536см³