1) sin 3x - sin 5x > 0
По формуле разности синусов

2sin(-x)*cos(4x) > 0
-2sin x*cos(4x) > 0
Делим на -2, при этом знак неравенства меняется.
sin x*cos(4x) < 0
Два варианта. Множители должны иметь разные знаки.
a)
{ sin x < 0
{ cos(4x) > 0
Решаем неравенства
{ x ∈ (-pi+2pi*k; 2pi*k)
{ 4x ∈ (-pi/2+2pi*k; pi/2+2pi*k); x ∈ (-pi/8+pi/2*k; pi/8+pi/2*k)
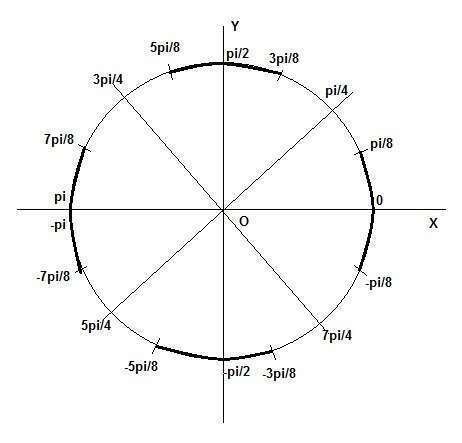
Решение 2 неравенства я показал на рисунке. Это жирные дуги.
Пересечение неравенств - это нижняя часть круга, где sin x < 0
x ∈ (-pi+2pi*k; -7pi/8+2pi*k) U (-5pi/8+2pi*k; -3pi/8+2pi*k) U (-pi/8+2pi*k; 2pi*k)
б)
{ sin x > 0
{ cos(4x) < 0
Решаем неравенства
{ x ∈ (2pi*k; pi+2pi*k)
{ 4x ∈ (pi/2+2pi*k; 3pi/2+2pi*k); x ∈ (pi/8+pi/2*k; 3pi/8+pi/2*k)
Решение 2 неравенства - это нежирные дуги на том же рисунке.
Пересечение неравенств - это верхняя часть круга, где sin x > 0
x ∈ (pi/8+2pi*k; 3pi/8+2pi*k) U (5pi/8+2pi*k; 7pi/8+2pi*k)
2) Про arcsin x - а где неравенство?