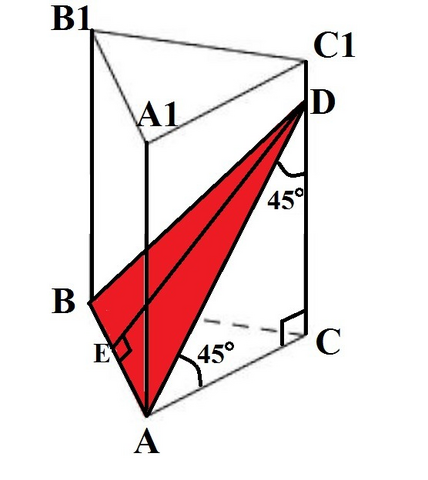
Основаниями правильной треугольной призмы ABCA1B1C1 являются равные правильные треугольники со стороной а.
Через сторону основания AB под углом 45° к плоскости основании призмы проведено сечение, пересекающее ребро CC1.
Треугольники DAC и DBC равны по двум сторонам и углу между ними:
AC=BC (как стороны правильного треугольника)
CD - общая сторона
∠ACD = ∠BCD = 90° (т.к. призма правильная)
⇒ AD = BD
⇒ сечение - равнобедренный треугольник с основанием AB
В прямоугольном треугольнике ACD:
∠ACD = 90°
∠DAC = 45°
∠ADC = 180 - 90 - 45 = 45 (°)
⇒ треугольник ACD - прямоугольный равнобедренный с основанием-гипотенузой AD, боковыми сторонами - катетами AC = DC = a
по теореме Пифагора:
AD² = AC² + DC²
AD² = a² + a²
AD² = 2a²
AD = a√2 (см)
В равнобедренном треугольнике ABD:
DE - высота, а также медиана и биссектриса, проведенная к основанию ⇒ AE = AB/2
AE = a/2
В прямоугольном треугольнике ADE:
Гипотенуза AD = a√2
Катет AE = a/2
По теореме Пифагора
AD² = AE² + DE²
(a√2)² = (a/2)² + DE²
DE² = 2a² - a²/4
DE² = 8a²/4 - a²/4
DE² = 7a²/4
DE = √(7a²/4)
a√7
DE = ---------- (см)
2
S(ABD) = 1/2 * a * DE
1 a√7 a * a√7 a²√7
S(ABD) = ------- * a * ---------- = --------------- = ------------ (см²)
2 2 2 * 2 4
Не соответствует ни одному из вариантов ответа.