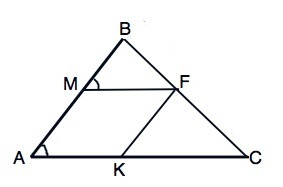
В треугольник ABC вписана ромб AMFK так, что угол A в них общий, а вершина F принадлежит стороне BC. Найдите сторону ромба, если AB = 10 см, AC = 15 см
--------
Примем сторону ромба равной х. Тогда в треугольнике МВF сторона МВ=АВ-АМ=10-х, сторона МF=x.
MF║AC, АВ - секущая. Соответственные ∠ВМF=∠ВАС, угол В - общий. ⇒треугольники АВС и МВF подобны. Из подобия следует отношение:
АВ:МВ=АС:MF
10:(10-х)=15:х ⇒
10х=150-15х
25х=150
х=6
Сторона ромба равна 6 см.