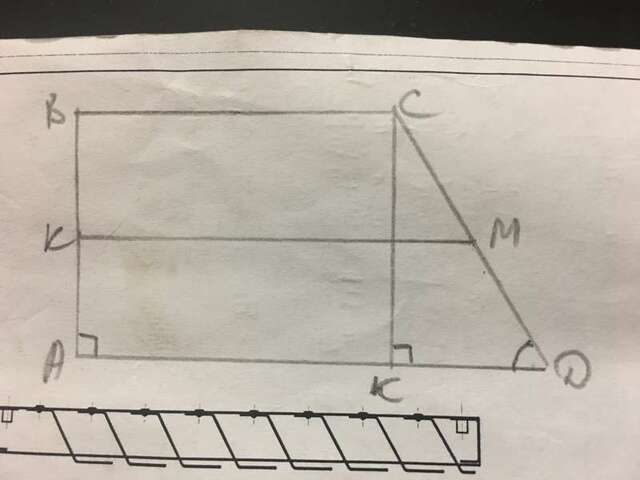
В трапеции АВСД АД=15 см, ВС=10 см. l=10 см.
Точка, равноудалённая от сторон трапеции, образует вместе с вершинами трапеции пирамиду, апофемы l которой равны, значит Основание высоты пирамиды лежит в центре вписанной в трапецию окружности.
Так как трапеция прямоугольная, то диаметр вписанной окружности равен высоте трапеции - её меньшей боковой стороне.
Пусть АВ=СК=х.
КД=АД-АК=АД-ВС=15-10=5 см.
СД=√(СК²+КД²)=√(х²+25).
В описанной трапеции суммы противолежащих сторон равны.
АД+ВС=АВ+СД,
15+10=х+√(х²+25),
25-х=√(х²+25), возведём уравнение в квадрат:
625-50х+х²=х²+25,
50х=600,
х=12.
Радиус вписанной окружности r=АВ/2=х/2=6 см.
В прямоугольном треугольнике, образованном высотой пирамиды, её апофемой и найденным радиусом, высота по т. Пифагора равна:
h=√(l²-r²)=√(10²-6²)=8 см - это ответ.