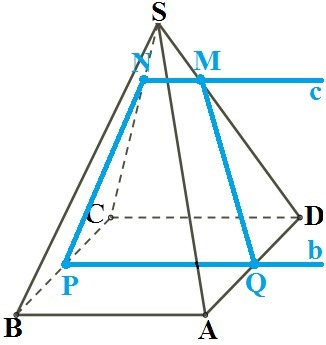
В основании правильной четыреухгольной пирамиды SABCD лежит квадрат, а боковые грани - равные равнобедренные треугольники.
Точка М не лежит на отрезке SO, т.к. такое сечение является треугольником с вершиной в точке S.
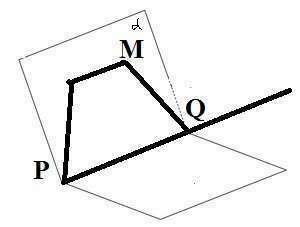
Точка М не лежит в плоскости основания пирамиды, т.к. через прямую и точку, которая не лежит на ней, можно провести только одну плоскость (теорема) ⇒ точка М отмечена на боковом ребре. Проводим плоскость α через точку М и отрезок PQ.
(ОФФТОП - без разницы на каком боковом ребре, возьмем для удобства SD)
Согласно теореме,
через точку (М), лежащую вне прямой *b* (которой принадлежит отрезок PQ) можно провести прямую, параллельную этой прямой, и к тому же только одну. Через точку М проводим прямую *с*, параллельную PQ. Прямая *с* и боковое ребро SC пересекаются в точке N.
PQ II MN и PQ II CD ⇒ СD II MN т.к.
Две прямые, параллельные третьей прямой, параллельные между собой (теорема)
Боковая грань SCD - равнобедренный треугольник с равными углами при основании ⇒ MNCD - равнобедренная трапеция.
Треугольники MDQ и NCP равны по двум сторонам и углу между ними:
MD = NC (как боковые стороны равнобедренной трапеции)
QD = PC (по условию)
∠MDQ = ∠NCP (как углы при основании равных равнобедренных треугольников)
⇒ MQ = NC
Четыреухгольник, у которого 2 стороны параллельны, а две другие стороны не параллельны и равны, является равнобедренной трапецией.