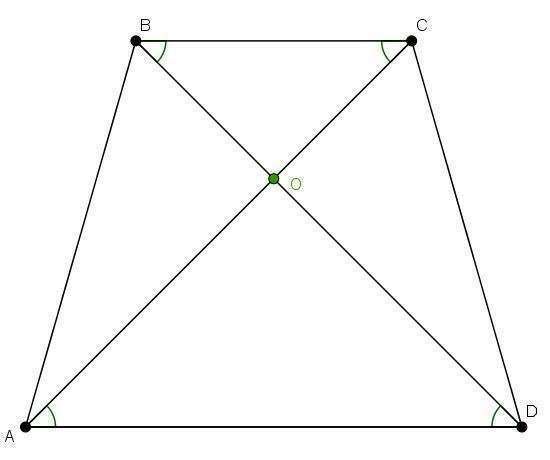
1. Зробимо малюнок.
2. Побудуємо діагоналі. O — точка їхнього перетину.
3. ∠DBC = ∠BDA як різносторонні при паралельних прямих BC і AD та січній BD.
4. ∠BCA і ∠DAC рівні за такою ж логікою. Отже, ∠DBC = ∠BCO.
5. Розглянемо ΔOBC. В нього два рівних кута, а отже, є рівними й сторони, що їм протилежні: BO=CO.
6. В ΔAOD за такою ж логікою AO=OD.
7. Розглянемо ΔABO і ΔDOC. В них BO=OC, AO=OD, а ∠BOA й ∠COD рівні як вертикальні. Отже, ці трикутники рівні за першою ознакою рівності, а отже, AB=CD, що і треба було довести.