Y=√(13-х)ln(7x-6) (все под корнем) найти область определения функции

$\sqrt{(13-x)*ln(7x-6)}$
Все, что под корнем должно быть больше либо равно 0:
$(13-x)ln(7x-6) \geq 0$
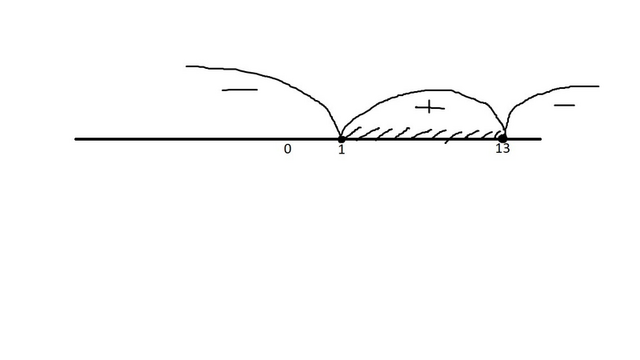
Для начала надо решить это неравенство(1 фото):
Находим нули функции,
$13-x=0\\ x = 13\\ ln(7x-6) = 0\\ 7x-6 = 1\\ 7x = 7\\ x = 1\\$
Осталось еще одно, все , что под логарифмом должно быть строго больше нуля:
$7x-6 \ \textgreater \ 0\\ 7x \ \textgreater \ 6\\ x \ \textgreater \ \frac{6}{7} \\$
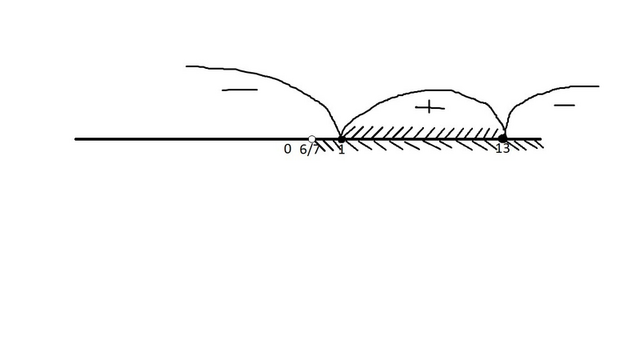
Итого получаем фото 2
На нем видно что пересечение всего того что нам нужно есть отрезок $[1;13]$
Ответ: $[1;13]$