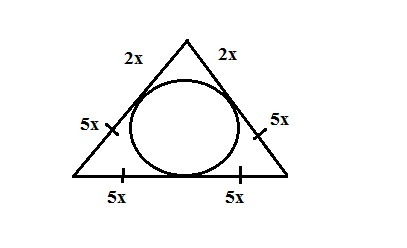2. Рассмотрим треугольники KDB и KTN.
1) KD=KT (по условию);
2) Угол KDB = угол KTN (по условию);
3) Угол DKT - общий.
Следовательно, треугольники KDB и KTN равны по II признаку.
Тогда BD=NT.
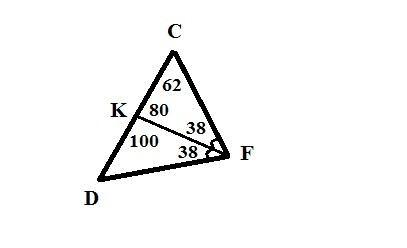
3. ∠ DKF + ∠FKC =180° (как смежные)
∠FKC =180°-∠ DKF=180°-100°=80°
В ΔFKC ∠FKC+∠KFC+∠KCF=180°
∠KFC=180°-∠FKC-∠KCF=180°-80°-62°=38°
∠KFD=∠KFC=38°, так как FK - биссектриса.
Тогда ∠ВАС=∠KFD+∠KFC=38°+38°=76°
4. P=a+2b
Воспользовавшись тем, что касательные к окружности, проведенные из одной точки, равны, получаем
a=10x b=7x (см. рисунок)
P=10x+2*7x=24x=72
x=72:24
x=3.
a=30 b=21
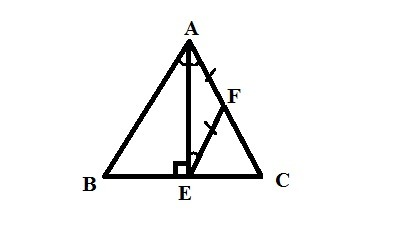
5. Так как AE - высота в равнобедренном треугольнике ABC, то AE - биссектриса, которая делит пополам угол A, то есть ∠BAF=∠EAC.
В равнобедренном треугольнике AFE (AF=FE по условию) углы при основании равны: ∠EAF=∠AEF. Тогда ∠AFE=∠BAF - это внутренние накрест лежащие углы, при прямых AB и EF и секущей AE. Так как внутренние накрест лежащие углы равны то прямые параллельны, то есть AB||EF, что и тр. док.