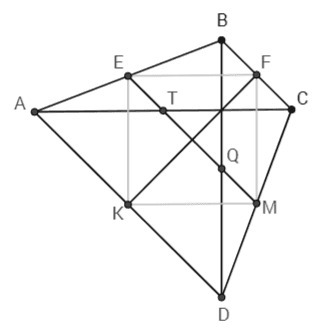
1) В треугольнике ABC средняя линия EF параллельна основанию AC и равна его половине. Анаголично KM||AC, EK||BD, FM||BD => EF||KM, EK||FM => EFMK - параллелограм.
AC⊥BD => EF⊥FM => EFMK - прямоугольник.
EF=КМ=AC/2, EK=FM=BD/2. Диагонали равнобедренной трапеции равны, AC=BD => EF=КМ=EK=FM => EFMK - квадрат.
2) SEFMK= EF^2 <=> EF= √SEFMK = √100 =10
AC=BD=2EF=10*2=20
SABCD= AC*BD/2 = 20*20/2 =200
3) FK - высота ABCD (вторая средняя линия в равнобедренной трапеции перпендикулярна основаниям).
FK - диагональ EFMK.
SEFMK= FK^2/2 <=> FK= √(2*SEFMK) = √(2*100) =10√2
4) Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии. TQ= (AD-BC)/2 =2√2
EM - диагональ EFMK. EM=FK
Средняя линия трапеции равна полусумме оснований. EM= (AD+BC)/2 =10√2
AD-BC =4√2
AD+BC =20√2
-----------
2AD=24√2 <=> AD=12√2
BC= AD-4√2 = 12√2 -4√2 =8√2