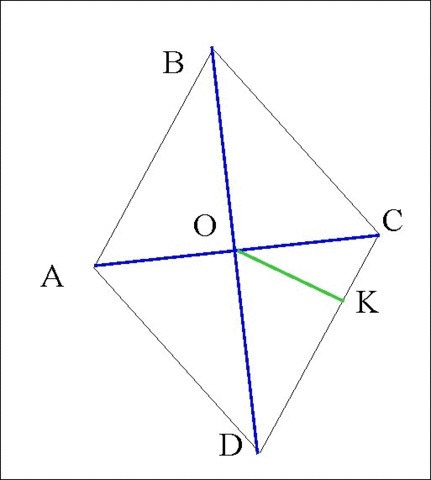
Дано:
АВСD - ромб
АС и ВD - диагонали.
ВD = 76
ОК ⊥DС
ОК = 19
Найти ∠А; ∠В; ∠С; ∠D.
Решеие:
Диагонали ромба всегда взаимно перпендикулярны и всегда точкой пересечения делятся пополам.
В прямоугольном ΔDОК катет ОК = 19,
гипотенуза DО = DВ/2 = 76/2=38.
Очевидно, что катет ОК равен половине гипотенузы DО
19 : 38 = 1/2, это означает, что напротив катета ОК лежит ∠ОDК, равный 30°.
∠ОDК= 30°.
Диагонали ромба всегда являются биссектрисами, значит, весь ∠АDC = 2·∠ODK = 2 · 30° = 60°.
∠ADC = ∠CBA = 60°.
∠BAD = ∠BCD = 180° - 60°=120°.
Ответ: 60°; 120°; 60°; 120°.