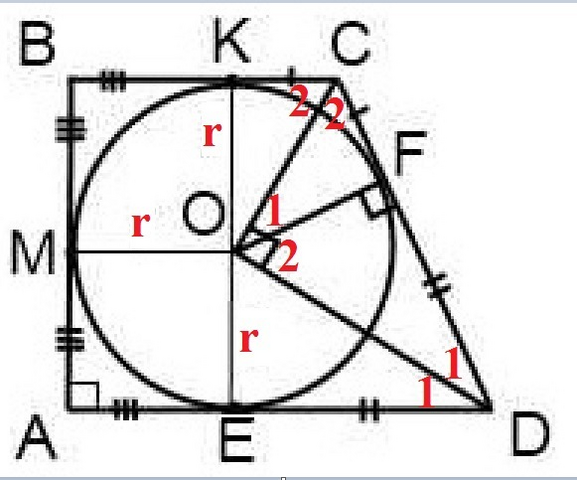
Пусть ABCD - прямоугольная трапеция, в которую вписана окружность с центром в т. О.
ВС - основание трапеции
AD - основание трапеции
∠A = 90°
DE = 16 см
AE = AM = BM = BK = KO = MO = EO = r = 12cм
AD = AE + DE
AD = 12 + 16 = 28 (cм)
В прямоугольном треугольнике ODE:
катет OE = 12см
катет DE = 16 см
OD - гипотенуза
по теореме Пифагора
OD² = OE² + DE²
OD² = 12² + 16² = 400
OD = √400 = 20 (см)
Свойство касательных: Отрезки касательных к окружности, проведенных из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности ⇒
⇒ ED = FD = 16cм и CK = CF как отрезки касательных, ОD - биссектриса ∠ADC, OC - биссектриса ∠BCD
Сумма углов трапеции, прилежащих к боковой стороне равна 180° ⇒
∠BCD + ∠ADC = 180° ⇒ ∠DCO + ∠CDO = 180 / 2 = 90 (°)
Сумма углов треугольника равна 180° ⇒
⇒ ∠COD = 180 - (∠DCO + ∠CDO ) = 180 - 90 = 90(°)
В прямоугольном треугольнике COD
∠OCD= 180 - 90 - ∠CDO ⇒ ∠OCD = 90 - ∠CDO
В прямоугольном треугольнике OFC
∠OCF = 180 - 90 - ∠COF = 90 - ∠COF ⇒ ∠CDO = ∠COF
В прямоугольном треугольнике DFO
∠DOF = 180 - 90 - ∠CDO = 90 - ∠CDO = ∠OCD
Треугольники DFO u OFC подобны по трем углам
∠DFO = ∠OFC = 90° т.к. радиус окружности, проеведенный в точку касания, перпендикулярен касательной
∠CDO = ∠COF
∠DOF = ∠OCD
У подобных треугольников углы равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника. ⇒
DO : OC = DF : OF = OF : CF
20 : OC = 16 : 12 = 12 : CF
16 : 12 = 12 : CF
Свойство пропорции: произведение крайних членов равно произведению средних
16СF = 12*12
16CF = 144
CF = 144 / 16
CF = 9 (cм), тогда CK = 9 см
BC = BK + CK
BC = 12 + 9 = 21 (cм)
Если в прямоугольную трапецию вписана окружность, ее площадь равна произведению оснований.
S = AD * BC
S = 28 * 12 = 336 (см²)
(не смогла нарисовать ровные дужки для обозначения равных углов, поэтому обозначила их цифрами)
....................................................................................................................