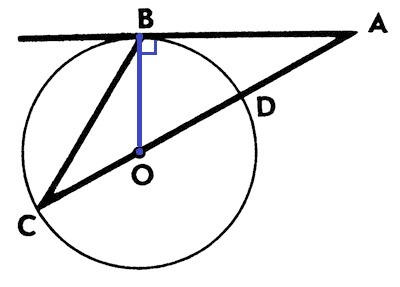
∠С - вписанный угол. Вписанный угол равен половине градусной меры дуги, на которую опирается. ∠С= ∪BD/2 = 62°/2 =31°
∠BOD - центральный угол. Центральный угол равен градусной мере дуги, на которую опирается. ∠BOD= ∪BD =62°
Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. AB⊥OB <=> ∠ABO=90°.
Сумма острых углов прямоугольного треугольника равна 90°.
∠A= 90°-∠BOD = 90°-62° =28°
Сумма углов треугольника равна 180°.
∠B= 180°-∠A-∠С = 180°-28°-31° =121°