1) В равностороннем △ABC ** биссектрисе ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC,...

Question

1) В равностороннем △ABC на биссектрисе ВН взята точка О так, что ON⊥BC; OM⊥AB (N∈BC, M∈AB). Докажите, что △ AOM=△NOC. Найдите углы этих треугольников.
2) В окружности с центром в точке О хорды АВ и СD пересекаются в точке N. ∠CNB=150°; CD⊥OB; CO⊥AB. Найдите ∠COB.
3) В △ABC AB=BC, на сторонах AB и АC отмечены точки К и Е так, что КЕ||ВС, KH – биссектриса ∠BKE; ∠BKH=32°. Найдите углы △ABC.

ПОЖАЛУЙСТА ПОМОГИТЕ ХОТЯ БЫ ОДНУ ЗАДАЧКУ!

Comments

Во второй задаче OB, CO - радиусы. Хорды перпендикулярны радиусам? Тогда они уже не хорды :)

Answer 1

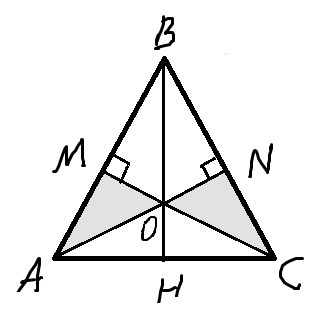
1) В равностороннем треугольнике высота (к любой стороне) является биссектрисой и медианой; высоты, биссектрисы, медианы (AN, BH, CM) пересекаются в одной точке (O).

∠OMA=∠ONC=90
∠MAO=∠NCO=∠BAC/2=60/30=30 (в равностороннем треугольнике все углы равны 60, высоты AN и CM являются биссектрисами)
∠AOM=∠NOC=90-30=60 (сумма острых углов прямоугольного треугольника равна 90)
AM=CN=AB/2 (AB=BC, высоты AN и CM являются медианами)
△AOM=△NOC (по стороне и прилежащим углам) 

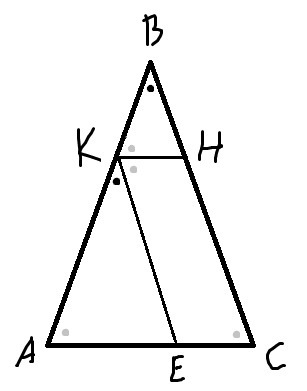
3) ∠AKE +2∠BKH =180 <=> ∠AKE=180-2*32=116 (∠AKB - развернутый угол, KH – биссектриса ∠BKE)
 ∠AKE=∠ABC=116 (соответственные углы при КЕ||ВС) 
∠ABC+ 2∠BAC =180 (в равнобедренном треугольнике углы при основании равны, сумма углов треугольника 180)
2∠BKH=180-∠AKE=180-∠ABC=2∠BAC
∠BKH=∠BAC=∠ACB=32

---

---