3. По условию V₁+V₂+V₃=V₄.
Объём шара: V=4πR³/3.
Пусть 4π/3=х, тогда:
x·R₁³+x·R₂³+x·R₃³=x·R₄³, x сокращается.
3³+10³+12³=2755,
R₄=∛2755≈14 см - это ответ.
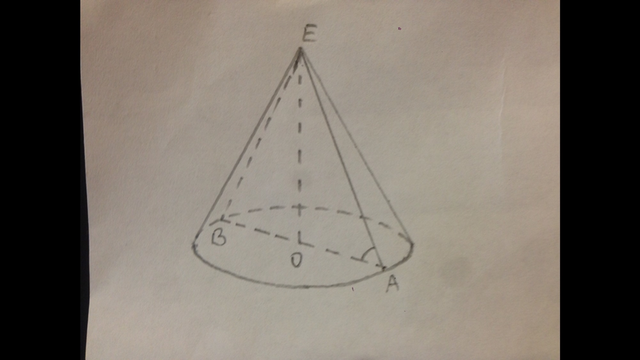
4. Площадь основания: So=πR² ⇒ R=√(So/π)=√(36π/π)=6 см.
Площадь боковой поверхности: Sб=S-So=96π-36π=60π см².
Sб=С·l/2=2πR·l/2=πRl, где l - образующая.
ЕА=l=Sб/(πR)=60π/(π·6)=10 см.
В прямоугольном треугольнике ЕАО ЕО=√(ЕА²-ОА²)=√(10²-6²)=8 см.
Объём конуса: V=So·h/3=36π·8/3=96π см³ - это ответ.