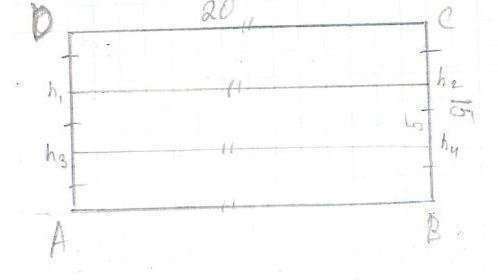Получается:
В прямоугольнике перпендикуляры к одной стороне, являются перпендикулярами и к другой, противоположенной - ну это ясно(думаю сможешь объяснить, объяснил ниже... на всякий случай) . => они делят и другую сторону на 3 равные части.
(далее см. чертеж)
РЕШЕНИЕ:
Сторона CB = 15см(по условию) => и сторона DA(т.к это прямоугольник, а прямоугольник это параллелограмм, а в нем противоположенные стороны попарно равны и параллельны).
Перпендикулярами разделен на 3 РАВНЫЕ части
=> 15\3=5(каждый отрезок)
Как мы уже и сказали перпендикуляры к одной стороне являются перпендикулярами и к другой(т.к это прямоугольник, а прямоугольник это параллелограмм, а в нем противоположенные стороны попарно равны и параллельны)
Вычислим большую сторону прямоугольника:
70-15*2=40\2=20 (это у нас стороны DC и AB)
Далее, у нас получаются равные прямоугольники.
С меньшей стороной 5 и большей 20.
Периметр меньшего прямоугольников(среди них нет меньшего, они все равны - следовательно берем любой) И назовем его h1h2h3h4
 =5*2+20*2=50см
=5*2+20*2=50см
Ответ:  =50 см
=50 см
Пойми и запиши короче, как считаешь нужным!
PS мог немного не понять задачу, так что лучше учись и решай сам. Это просто, главное знать теоремы.