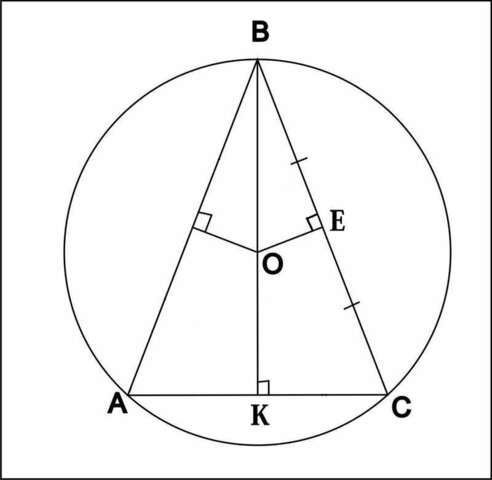
ABC - равнобедренный треугольник с основанием AC, боковыми сторонами AB=BC= 16 cм
Около треугольника описана окружность с центром в т. O. Центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров ⇒ BE = CE ⇒ BE = BC/2 = 16/2 = 8 (cм)
Расстоянием от боковой стороны треугольника ABC до центра окружности является перпендикуляр OE = 6 cм
В прямоугольном теругольнике BEO:
BE= 8cм - катет
OE= 6cм - катет
BO - гипотенуза
по теореме Пифагора:
BE² + OE² = BO²
8² + 6² = BO²
64 + 36 = BO²
BO² = 100
BO = 10 (cм)
Расстояние от вершины треугольника до центра, описанной около этого треугольника окружности, равно радиусу этой окружности ⇒
BO = R = 10 cм
Радиус описанной окружности равнобедренного треугольника вычисляется по формуле:
a²
R= --------------------
√(4a² - b²)
где R - радиус описанной окружности
а - боковая сторона равнобедренного треугольника
b - основание равнобедренного треугольника
BC²
R= -----------------------------
√(4BC² - AC²)
√(4BC² - AC²) = BC² / R
√(4 * 16² - AC²) = 16² / 10
√(4* 256 - AC²) = 256 / 10
√(1024 - AC²) = 25,6
1024 - AC² = 25,6²
1024 - AC² = 655,36
1024 - 655,36 = AC²
AC² = 368,64
AC = √368,64
AC = 19,2 (cм)
BK является высотой, биссектрисой и медианой, проведенной к основанию равнобедренного треугольника ⇒ AK=CK=AC/2
CK = 19,2 / 2 = 9,6 (cм)
В прямоугольном треугольнике BCK:
BC= 16 см - гипотенуза
CK= 9,6 cм - катет
BK - катет
по теореме Пифагора:
BK² + CK² = BC²
BK² + 9,6² = 16²
BK² + 92,16 = 256
BK² = 256 - 92,16
BK² = 163,84
BK = √163,84
BK = 12,8 (cм)