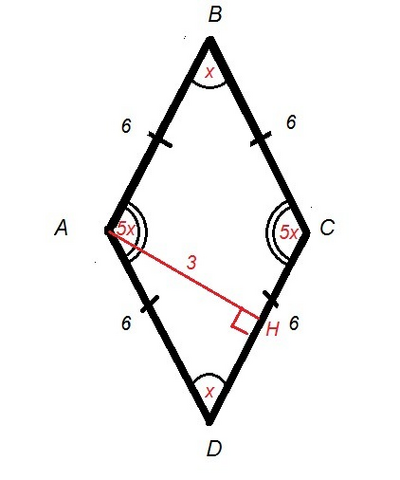
Ромб АВСD , по свойствам ромба:
Стороны равны
АВ=ВС=СD=DА = 6 см
Противолежащие углы равны
∠В = ∠D = x° (острые углы)
∠A=∠C = 5x° (тупые углы)
Сумма углов прилежащих к одной стороне равна 180°, следовательно:
х + 5х = 180
6х = 180
х = 180 :6
х = 30° ⇒ ∠В=∠D = 30°
∠A=∠C = 5*30 = 150°
Площадь ромба:
1) через сторону и угол : S=a²*sinα
S= 6²* sin30°= 36 * ¹/₂ = ³⁶/₂ = 18 (см²)
2) через сторону и высоту : S=ah
S=ah
Проведем высоту АН (∠Н= 90°) ⇒Δ АНD - прямоугольный
AD=6 см - гипотенуза
АН, НD - катеты
∠D = 30°
Катет, лежащий против угла в 30° равен половине гипотенузы
АН = AD/2 ⇒ АН = 6/2 = 3 см
S = 6 * 3 = 18 (см²)
Ответ: S = 18 см².