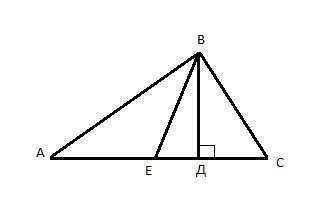
Построим произвольный прямоугольный треугольник АВС. Проведем
из прямого угла АВС высоту ВД и медиану ВЕ.
Наибольшим углом данного треугольника будет ∠АВС=90
градусам.
Найдем наибольший
ОСТРЫЙ угол данного треугольника:
По условию ∠ДВЕ=3 °.
Рассмотрим треугольник ВДЕ:
∠ВЕД=180-ВДЕ-ДВЕ=180-90-3=87 °.
∠ВЕА=180-ВЕД=180-87=93
°(как смежные углы).
Так как медиана, проведенная из вершины прямого угла, равна половине
гипотенузы мы получаем два равнобедренных треугольника:
ВАЕ и ВСЕ
Рассмотрим треугольник ВАЕ:
так как АЕ=ВЕ то углы ВАЕ=АВЕ (углы при
основании равнобедренного треугольника)
Значит ∠ВАЕ=(180-ВЕА)/2=(180-93)/2=43,5°
Рассмотрим треугольник ВСЕ:
так как СЕ=ВЕ то углы ВСЕ=СВЕ (углы при
основании равнобедренного треугольника)
Значит ∠ВСЕ=(180-ВЕС)/2=(180-87)/2=
46,5°
43,5<46,5</p>
А значит, наибольшим острым углом
треугольника АВС является угол ВСА=46,5 градуса