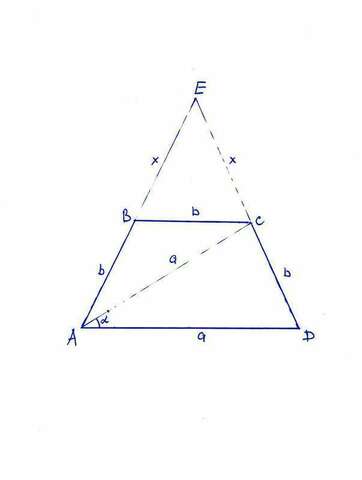
Все обозначения на чертеже, пояснять, что есть что - не буду.
Из подобия треугольников ADE и BCE следует
x/b = (x + b)/a;
что означает, что AC делит ED пропорционально AD и AE, то есть AC - биссектриса угла EAD.
Далее, угол BCE = угол ADE, следовательно, оба треугольника BCE и ACD - равнобедренные, имеют равные углы при основании и равные основания, так как BC = CD.
Таким образом, x = BE = EC = a;
Итак, в равнобедренном треугольнике AED основание AD = биссектриса AC = отрезок от вершины до основания биссектрисы EC. Этот треугольник полезно запомнить - и сейчас станет ясно, почему.
Если обозначить угол CAD = α; то теперь очевидно,
что угол CDA = угол ACD = 2α; (AC - биссектриса угла А, и не надо забывать, что и трапеция равнобедренная). Угол BCA = α; поэтому угол BCD = 3α; и
5α = 180°; откуда α = 36°;
углы трапеции равны 108° и 72°; это ответ :)
а теперь - почему так устроенный треугольник AED так важен.
Поскольку x = a; то (a + b)/a = a/b;
если обозначить b/a = y; то 1 + y = 1/y; или y^2 + y - 1 = 0;
откуда y = (√5 - 1)/2;
Отсюда получается cos(72°) = (a/2)/(a + b) = (1/2)/(1 + b/a) = 1/(2 + 2y) = 1/(√5 + 1) = (√5 - 1)/4;
cos(72°) = (√5 - 1)/4; то есть получено выражение в радикалах для косинуса угла 72°; конечно же, cos(72°) = sin(18°); и это означает, что получены выражения в радикалах для всех углов, кратных 18° (ну, я их вычислять тут не буду, это и не важно).