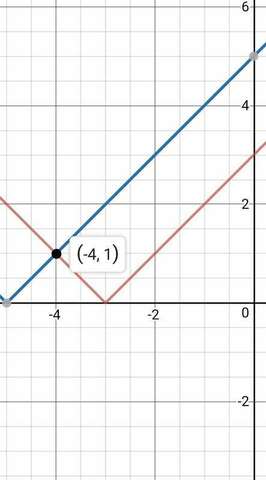
1) графически:
надо построить графики функций y=|x+3| и y=|x+5|, тогда координата x их точки пересечения будет корнем этого уравнения:
1) y=|x+3|
x=-3; y=0
x=0; y=3
x=-4; y=1
x=1; y=4
2) y=|x+5|
x=-5; y=0
x=0; y=5
x=-6; y=1
x=1; y=6
графики в приложении: красным цветом - функция y=|x+3|, синим - y=|x+5|
эти графики пересекаются в точке (-4;1) откуда следует, что уравнение имеет 1 корень x=-4
2) аналитически:
1)x+3=x+5, x+3>=0; x>=-3 и x+5>=0; x>=-5
0x=-2
x - нет корней
2)-x-3=x+5, x<=-3 и x>=-5
-2x=8
x=-4 - верно
3) x+3=-x-5, x>=-3 и x<=-5<br>x - нет корней
4) -x-3=-x-5, x<=-3 и x<=-5<br>0x=-2
x - нет корней
в итоге получили 1 корень: x=-4
Ответ: x=-4