Решите уравнение Lg (x+3) = 3 + Lg5

$\cfrac{x^2-14x-15}{10-4x}\ \textgreater \ 0\ \textless \ =\ \textgreater \ \cfrac{x^2-14x-15}{4x-10}\ \textless \ 0\ \textless \ =\ \textgreater \ \cfrac{x^2-14x-15}{x-2,5}\ \textless \ 0$

разложим числитель на множители (такое надо делать в первую очередь, кстати): $x^2-14x-15=0$ , тогда, по теореме Виета, первый и второй корни равны –1 и 15 соответственно, следовательно, $x^2-14x-15=(x-15)(x+1)$

преобразовав исходное неравенство, мы получили следующее: $\cfrac{(x-15)(x+1)}{x-2,5}\ \textless \ 0$

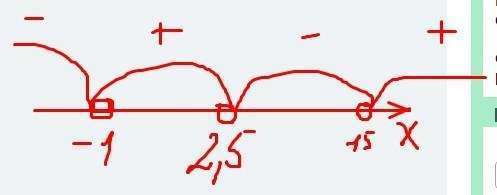
отмечаем точки на координатной прямой, изображаем интервалы, расставляем знаки и пишем ответ: x∈(–∞; –1)∪(2,5; 15)

$lg(x+3)=3+2lg5\\lg(x+3)-2lg5=3\\lg(\frac{x+3}{25})=3\\\frac{x+3}{25}=10^3\\x+3=10^3*25\\x=2,5*10^4-3=24997$