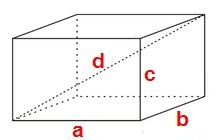
Задание. В прямом параллелепипеде стороны основания 3 и 6 см угол между ними 30градусов. площадь боковой поверхности равна 24 см²
. вычислить объем этого параллелепипеда.
Решение:
Поскольку в основании лежит параллелограмм, стороны 
, то площадь основания равен

см².
Площадь боковой поверхности:

Объем параллелепипеда:

см³
Ответ: 12 см³.