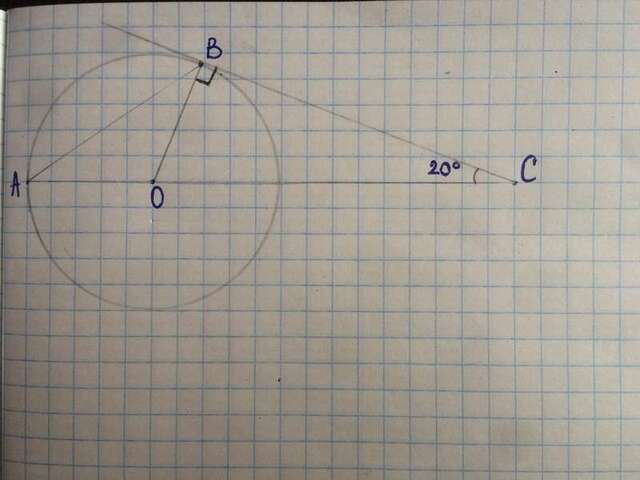
Рассмотрим ΔСВО. ∠СВО = 90° (касательная к окружности перпендикулярна к радиусу, проведенному в точку касания). ∠ВОС = 90°-∠ВСО=90°-20°=70°.
∠АОВ и ∠ВСО смежные, а, следовательно, их сумма равна 180°. Тогда ∠АОВ = 180°-∠ВОС=180°-70°=110°.
Рассмотрим ΔАОВ. Он равнобедренный: ОА=ОВ (радиусы). Тогда ∠ОАВ=∠ОВА=(180°-∠АОВ):2=(180°-110°):2=35°
То есть мы получили: ∠АОВ=110°; ∠АВО=35°; ∠ВАО=35°