В основании прямой призмы лежит ромб с диагоналями 16 см и 30 см а диагональ боковой...

Question

В основании прямой призмы лежит ромб с диагоналями 16 см и 30 см а диагональ боковой грани призмы образует с основанием угол 60 градусов Найдите площадь боковой поверхности призмы

Answer 1

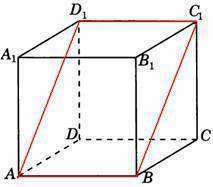
Дано: Призма прямая в основании ромб ABCD.
АС=d1=30 BD=d2=16. ∠ C1BC=60°
 Sбок=?
Решение:
Основание ромб значит:
4a²=d1²+d2²
a= √(d1²+d2²)/4
a= √(30²+16²)/4=√(900+256)/4=√1156/4=√289=17
a=17
По теореме синусов находим высоту призмы
h=17sin60/sin30=(17*√3/2)/0.5=17√3
Sбок=4аh
Sбок=4*17*17√3= 1156√3

---