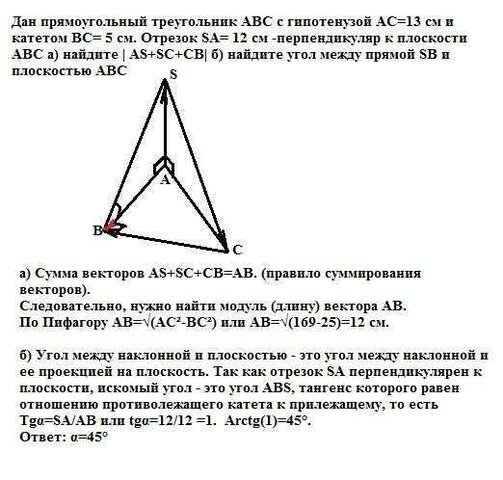
А) Сумма векторов AS+SC+CB=AB. (правило суммирования векторов).
Следовательно, нужно найти модуль (длину) вектора АВ.
По Пифагору АВ=√(АС²-ВС²) или АВ=√(169-25)=12 см.
б) Угол между наклонной и плоскостью - это угол между наклонной и ее проекцией на плоскость. Так как отрезок SA перпендикулярен к плоскости, искомый угол - это угол АВS, тангенс которого равен отношению противолежащего катета к прилежащему, то есть
Tgα=SA/AB или tgα=12/12 =1. Arctg(1)=45°.
Ответ: α=45°