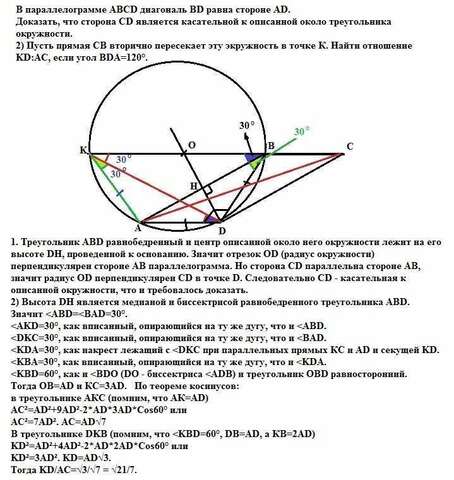
1. Треугольник ABD равнобедренный и центр описанной около него окружности лежит на его высоте DH, проведенной к основанию.
Значит отрезок OD (радиус окружности) перпендикулярен стороне АВ параллелограмма. Но сторона CD параллельна стороне АВ, значит радиус OD перпендикулярен CD в точке D.
Следовательно CD - касательная к описанной окружности, что и требовалось доказать.
2) Высота DH является медианой и биссектрисой равнобедренного треугольника ABD. Значит Тогда ОВ=AD и КС=3AD. Тогда по теореме косинусов:
в треугольнике АКС (помним, что АК=АD)
АС²=AD²+9AD²-2*AD*3AD*Cos60° или
АС²=7AD². AC=AD√7
В треугольнике DKB (помним, что KD²=AD²+4AD²-2*AD*2AD*Cos60° или
KD²=3AD². KD=AD√3.
Тогда KD/AC=√3/√7 = √21/7.