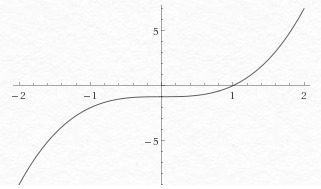
Y=x^3-1
D(y)=(-00,+00)
E(y)=(-00,+00)
y(-x)=(-x)^3-1=-x^3-1 функция общего порядка
непереодичная
y=0
x^3-1=0 x=1
(1;0) - нуль функции
y>0
x^3-1>0
(x-1)(x^2+x+x^2)>0 x^2+x+x^2>0 при всех x тк D<0(-3)<br> - 0 +
y положительная на (0,+00), отрицательна на (-00,0]
y`=3x^2
3x^2=0
xmin=0
y`>0 при все x≠0 ⇒ y монотонно возрастающая функция
y``=6x
6x=0
x=0
(0;-1) -точка перегиба
y``
- 0 +
y выпукла вогнута
асимптот нет
x0 1 2 -2
y-1 0 7 -9