Чтобы аналитически проверить, пересекаются ли графики функций, нужно решить уравнение:
||x - 1| - 1| = 1
Раскрываем внешний модуль:
1) со знаком "+"
|x - 1| - 1 = 1
|x - 1| = 2
x - 1 = 2 или x - 1 = -2
x = 3 или x = -1
2) со знаком "-":
|x - 1| - 1 = -1
|x - 1| = 0
x = 1
Ответ: да, причём в трёх точках.
y = ||x - 1| - 1|.
Этапы построения:
1) Строим график функции y = x - 1.
2) Отражаем зеркально от оси Ox ту часть графика, которая лежит ниже оси Ox.
3) Переносим то, что получилось, на 1 ед. вниз.
4) Снова отражаем ту часть графика зеркально от оси Ox, которая лежит ниже этой оси.
Таблица точек для y = x - 1:
x 1 2
y 0 1
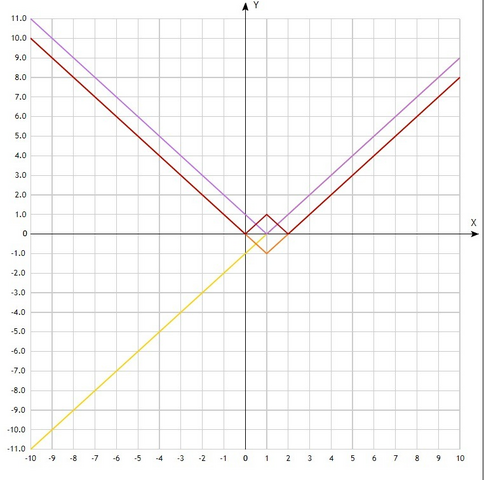
Графики во вложении (жёлтый - y = x - 1; розовый - y = |x - 1|; оранжевый - y = |x - 1| - 1; красный - y = ||x - 1| - 1|).