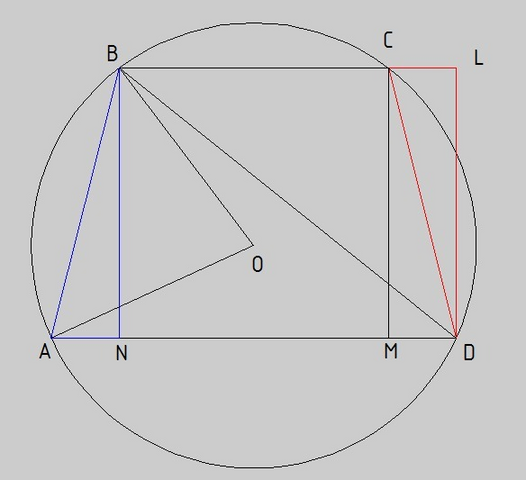
1. Достроим трапецию красным треугольником СLD и докажем, что он равновелик треугольнику ANB
Треугольник ANB равен треугольнику CMD и треугольнику CLD т.к. у них все три угла соответственно равны, и высота трапеции - является катетом и каждом треугольнике.
Из равенства красного и синего треугольника следует равенство площадей трапеции ABCD и прямоугольника BLDN
2
Центральный угол АОВ, под которым видна боковая грань трапеции АВ, в два раза больше вписанного угла АDB
Угол АОВ дан по условию, высота BN дана по условию, вычисляем площадь прямоугольника BLDN
BN/ND = tg (AOB/2)
ND = BN/tg(AOB/2)
s = BN * ND = BN * BN / tg (AOB/2)
Ответ: Площадь трапеции будет равна