1. Периметр параллелограмма равен 40 дм, а одна из диагоналей-8 дм. Найдите периметр...

Question

35 просмотров

1. Периметр параллелограмма равен 40 дм, а одна из диагоналей-8 дм. Найдите периметр треугольника, ограниченного этой диагональю и сторонами параллелограмма. 2. Боковая сторона равнобедренного треугольника = 4 см, а угол при основании - 30 градусов. Найдите радиус окружности, описанной около этого треугольника 3. Постройте острый угол, синус которого равен 3/5. поже

Геометрия Serega1546_zn (24 баллов) 17 Май, 18 | 35 просмотров

Дан 1 ответ

kirillsawkin_zn · Answer 1 · 2018-05-17T06:52:53+0000

1. Диагональ параллелограмма делит его на два равных треугольника, а так как противоположные стороны параллелограмма равно, то можно предположить, что периметр этих двух треугольников равен, следовательно 40 делим на 2 равно 20. Периметр это сумма длин всех сторон, а так как две стороны треугольника равны сумме 20, а диагональ по усл. равно 8, то 20+8=28
2.Допустим треугольника АВС. АС- основание. Проведем высоту ВН. Т.к. треугольник равнобедренный, она (высота) будет являться медианой и биссектрисой. Получили два прямоугольных треугольника: АВН и НВС. АН=НС 4дм/2дм=2дм. По теореме Пифагора ищем АН.
√4²-2²=√12=2√3 дм. Это и будет являться радиусом описанной окружности.
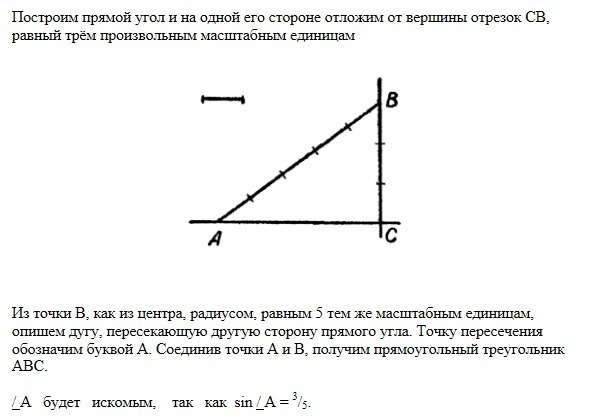
3. Номер три на фотке
P.S. за 3 задания 5 балов маловато, побольше бы :)