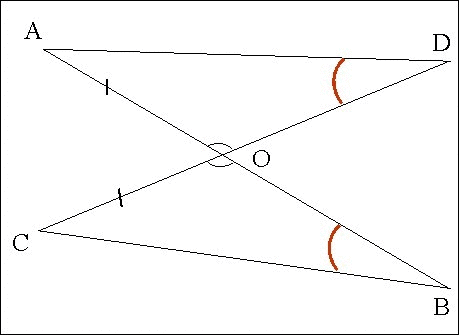
рисунок ниже
Дано: АВ и CD - прямые
О - точка пересенения
AB = CD
AO = CO
Доказать: а) Δ BOC= Δ DOA
б) ∠ ABC = ∠ADC
Доказательство:
а).
1) AB = CD - по условию
AO = CO - по условию
От равных отрезков отнимем равные отрезки, получим отрезки, равные между собой.
AB-AO = CD-CO
OB = OD
2).
Получаем, равенство треугольников Δ BOC= Δ DOA по двум сторонам и углу между ними.
AO = CO - по условию
OB = OD - доказано в первом действии
∆BOC= ∆ DOA - равенство треугольников доказано.
б) Из равенства ∆BOC= ∆ DOA
следует равенство соответственных углов, т.е.
< ОBC=
< DAО=<ОCВ;</p>
Из равенства углов < ОBC=
следует равенство соответственных углов, т.е.
< ABC=