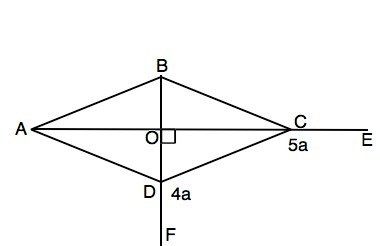
Примем коэффициент отношения данных углов равным а.
Тогда ∠FDC=4a; ∠ECD=5a
Угол ОDF развернутый, ⇒ угол ODC=180°-4a
Угол ОСЕ - развернутый ⇒ угол ОСD=180°-5а.
Диагонали ромба пересекаются под прямым углом и делят углы ромба пополам.
∆ DOC прямоугольный.
Сумма острых углов прямоугольного треугольника =90°.
180°-4а+180°-5а=90°
9а=270° ⇒
а=30°
Угол ВDC=180°-4•30°=60°
Противолежащие углы ромба равны.
Угол АВС=АDC=2•∠BDC=120°
Сумма углов. прилежащих к одной стороне параллелограмма, равна 180°⇒
угол ВАD=BCD=180°-120°=60°