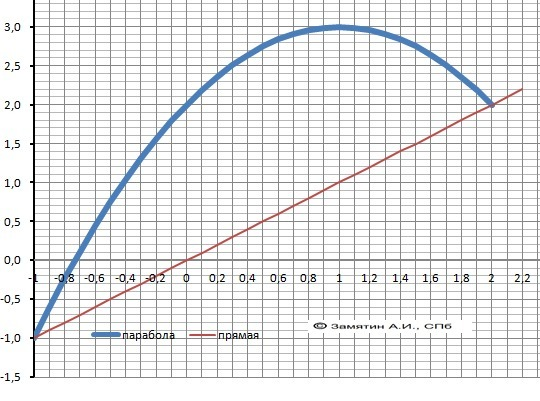
Делаем графическое решение задачи - в приложении.
ДАНО
F(x)=x
G(x) = - x²+2x+2
НАЙТИ
S(F,G)=? - площадь пересечения графиков.
ДУМАЕМ
Площадь - интеграл (первообразная) функции.
РЕШЕНИЕ
Находим точки пересечения графиков - пределы интегрирования.
1) -x²+2x+2 = x
- (x+1)*(x-2)=0
Корни уравнения - х1 = -1 и х2 = 2 - пределы интегрирования.
2) Площадь фигуры - разность интегралов. Парабола выше - из неё и вычитаем.
S(F,G) = G(x)dx - F(x)dx = (-x²+2x+2)dx - x*dx = -1/3*x³ +1/2*x²+2x
Вычисляем подставив пределы интегрирования.
S(-1) = -1 1/6, S(2)= 3 1/3
S = 3.333 - (-1.667) = 4.5 - площадь - ОТВЕТ